how to find the angle of a triangle

Angle is measured in degrees (°) and radians. Information technology is formed betwixt the 2 adjacent sides of a polygon. Every polygon has different sides and unlike numbers of angles. The formula to observe the angles in degrees is useful in geometry and trigonometry. It is essential to understand other concepts of mathematics, such as arc, a central angle of the circle, etc.

A total circle = 360°
A directly line = 180°
A semicircle= 180°
A Quarter circle = 90°

Calculating angles in degrees

At that place are 3 different methods of finding angles in degrees, which are as follows:

Using the protector D
Using the Pythagoras theorem and trigonometry function ins a correct angle triangle
Using the sum of angles formula
Central bending of a circle

Using the protector D

A protector is a type of ruler or scale that is used to measure distance in centimeters or millimeters. The protector used to measure angles is in a shape of 'D' with the value of angles marked from 0 to 180 ° from either direction (right or left). Nosotros need to marshal the axis with the line on the D to measure the angle. The heart circle of the protector is aligned to the vertex of the bending being measured. The rays along the vertex of angle volition help to find the angle in degrees.

Using the Pythagoras theorem and trigonometry function in a correct angle triangle

In trigonometry, in that location are half-dozen functions, sine, cos, cosec, tan, cot, and sec. A right-angle triangle has 3 sides, base, perpendicular, and hypotenuse.

Base: It is an side by side side to the angle of xc°.
Perpendicular: It is as well an adjacent side to the angle of 90°.
Hypotenuse: Information technology is a side contrary to the bending of ninety°.

A right-bending triangle is represented by an bending of ninety° as one of the angles. The full sum of the bending of a triangle is 180°.

Cosecθ: It is represented as hypotenuse divided by perpendicular.

Cosecθ = $\frac{hypotenuse}{perpendicular}$

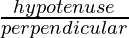
Cotθ: It is represented as base of operations divided past perpendicular.

Cotθ = $\frac{base}{perpendicular}$

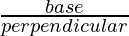
The other trigonometric functions are represented every bit:

sinθ = $\frac{perpendicular}{hypotenuse}$

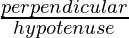
Cosθ = $\frac{base}{hypotenuse}$

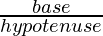
tanθ = $\frac{perpendicular}{base}$

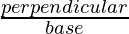
secθ = $\frac{hypotenuse}{base}$

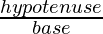
Cosecθ can too be represented as 1/ sinθ

secθ tin can too exist represented as 1/ cosθ

Cotθ tin can also exist represented as 1/ tanθ

Where,

Θ is the angle

Pythagoras Theorem

If two sides of a correct bending are known, we can hands calculate the third side of a right angle triangle. In a right-angled triangle, Pythagoras theorem is given by:

(Hypotenuse)² = (Base)² + (perpendicular)²

Sum of angles formula

The Sum of angles refers to the total sum of internal angles of a polygon forming between the two sides. If in that location are half dozen sides of a polygon, there are around six angles. It helps to detect an angle if other angles and the sum of angles of a polygon is known.

The formula to find the full sum of angles of a polygon is given by:

Total sum of angles = 180 (n – ii)

Where,

n is the number of sides of a polygon

Instance:

If n = iv,

Total sum of angles = 180 (4 – two)

= 180 (2)

= 360 °

If n = 5,

Total sum of angles = 180 (v – 2)

= 180 (3)

= 540 °

If n = six

Full sum of angles = 180 (vi – 2)

= 180 (iv)

= 720°

Key angle of a circle

A circle is a round shape figure whose boundary is equidistant from its center point. The altitude between the eye point and the boundary is known as the radius of the circle. The angle formed by the 2 radii of the circle is known equally the primal angle. The value of the fundamental bending of a circle lies between 0 and 360 degrees.

The formula to calculate the centre angle of a circumvolve is given past:

Length of arc = 2πr × (θ/360)

Θ = 360L/2πr

Where,

r is the radius of the circumvolve

AB is the arc

Theta is the angle in degrees.

50 = Arc length

Sample Problems

Question one: Observe the primal angle of a circle of radius 2m with an arc length of 4m?

Solution:

The formula to summate the centre bending of a circumvolve is given by:

Θ = 360L/2πr

Where,

r is the radius of the circle

Theta is the bending in degrees.

L = Arc length

Θ = Bending in degrees

r = 2m

L = 4m

Θ = 360 × 4 /2× π × two

Θ = 114.half dozen°

Thus the key bending of the circle is 114.half-dozen°.

Question 2: Find the cardinal angle of a circle of radius 10cm with an arc length of 18cm?

Solution:

The formula to calculate the center angle of a circumvolve is given by:

Θ = 360L/2πr

Where,

r is the radius of the circle

Theta is the bending in degrees.

Fifty = Arc length

r = 10cm

L = 18cm

Θ = Angle in degrees

Θ = 360 × 18 /2 × π × 10

Θ = 103.xiii°

Thus the central angle of the circle is 103.thirteen°.

Question 3: Find the angle of a parallelogram if the other 3 angles are 80°, 95°, and 105°?

Solution:

There are iv sides in a parallelogram with the total sum of angles 360°.

Formula to find the sum of angles = 180 (due north – ii)

Where,

n is the number of sides of a polygon

Here, northward = iv,

The total sum of angles = 180 (4 – 2)

= 180 (2)

= 360 °

Total sum = Angle ane + Angle ii + Bending three + Angle 4

360 = 80+ 95+ 105+ Angle iv

360 = 280 + Bending 4

Angle iv = 360 – 280

Bending 4 = 80°

Question 4: Find bending A in the given effigy.

Solution:

Given: Hypotenuse = 12

Perpendicular = 6

The trigonometry function to calculate the angle is given by:

sinA = 6/12

A = 30°

Question 5: Find bending A in the given figure.

Solution:

Given: Hypotenuse = 10

Base= five

The trigonometry function to calculate the bending is given by:

CosA = five/x

A = 60°

Question six: Discover the angle of a pentagon if other four angles are 115°, 100°, 105°, and 100°?

Solution:

There are v sides in a pentagon with the full sum of angles 540°.

Formula to observe the sum of angles = 180 (due north – ii)

Where,

n is the number of sides of a polygon

Here, n = 5,

Total sum of angles = 180 (5 – two)

= 180 (3)

= 540°

Total sum = Angle 1 + Angle ii + Bending 3 + Angle 4 + Angle 5

540 = 115° + 100° + 105°+100° + Bending 5

540 = 420 + Angle 5

Angle five = 540 – 420

Angle 5 = 120°

Question 7: Discover bending A in the given effigy.

Solution:

Given: Base = √3

Perpendicular= 1

The trigonometry role to calculate the angle is given past:

tanθ = $\frac{perpendicular}{base}$

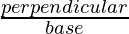
tanθ = ane/√iii

A = 30°

Question eight: Notice the angle of a parallelogram if other 3 angles are 100°, lxx° and 80°?

Solution:

There are four sides in a parallelogram with the total sum of angles 360°.

Formula to find the sum of angles = 180 (n – two)

Where,

n is the number of sides of a polygon

Here, northward = four,

Total sum of angles = 180 (4 – ii)

= 180 (2)

= 360°

Full sum = Angle i + Angle 2 + Angle 3 + Angle 4

360 = 100 + 70 + fourscore + Angle 4

360 = 250 + Angle 4

Bending 4 = 360 – 250

Angle four = 110°

Thus, the other angle is 110°.

Question 9: Find the angle of a hexagon if other five angles are 120°, 115°, 110°, 125°, and 105°?

Solution:

In that location are six sides in a hexagon with the total sum of angles 720°.

Formula to find the sum of angles = 180 (6 – two)

Where,

n is the number of sides of a polygon

Here, n = six,

Total sum of angles = 180 (six – 2)

= 180 (4)

= 720°

Full sum = Bending one + Angle ii + Angle 3 + Angle 4 + Angle v + Angle 6

720 = 120 + 115 + 110 + 125 + 105 + Angle 6

720 = 575 + Angle 6

Angle half-dozen = 720 – 575

Angle six = 145°

Thus, the 6th angle of hexagon is 145°.