How To Find The Volume Of A Triangular Prism How To Find The Volume Of A Triangular Prism

Triangular Prism Calculator

Created by Hanna Pamuła , PhD candidate and Jasmine J Mah

Reviewed by

Bogna Szyk and Jack Bowater

Final updated:

Sep 23, 2021

Tabular array of contents:

• Triangular prism - what's that?
• Triangular prism formulas
• Triangular prism volume
• Triangular prism surface area
• How to observe the book of a triangular prism with this tool?
• FAQ

If you ever wondered how to discover the volume of a triangular prism, this triangular prism figurer is the thing you are looking for. Not only can information technology summate the volume but also may be helpful if you need to determine the triangular prism surface area. Choose the pick which fits your needs and experiment with the tool! If you are curious virtually triangular prism formulas behind the calculator, scroll downwards to notice out more.

Triangular prism - what's that?

What is a prism? Information technology'south a solid object with:

• identical 2 bases
• iii rectangular faces (right prism) or in parallelogram shape (oblique prism)
• the same cantankerous section forth its whole length

We are using the term triangular prism to depict the right triangular prism, what is quite a mutual practice. If you are looking for other prism blazon, cheque our rectangular prism figurer.

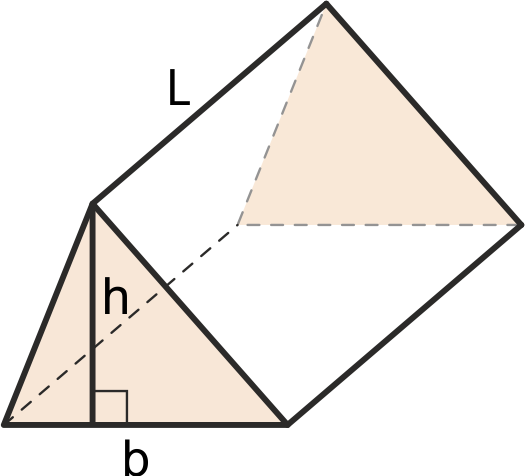
Triangular prism formulas

Usually what y'all need to calculate are the triangular prism volume and its expanse. The ii most basic equations are:

• volume = 0.5 * b * h * length, where b is the length of the base of the triangle, h is the height of the triangle and length is prism length

• expanse = length * (a + b + c) + (2 * base_area), where a, b, c are sides of the triangle and base_area is the triangular base area

But what if we don't have the pinnacle and base of the triangle? And how to find triangular prism surface expanse without all sides of the triangular base? Check out the other triangular prism formulas!

Triangular prism volume

In the triangular prism calculator you tin hands find out the book of that solid. A general formula is volume = length * base_area; the one parameter you ever need to accept given is the prism length, and there are four ways to calculate the base of operations - triangle expanse. Our triangular prism computer has all of them implemented, isn't information technology awesome?

The specific formulas wait as follows:

• Length * Triangular base area given triangle base of operations and height

  It'southward this well-known formula mentioned before:

  volume = length * 0.5 * b * h

• Length * Triangular base area given three sides (SSS)

  If you know the lengths of all sides, use the Heron's formula to find the surface area of triangular base:

  book = length * 0.25 * √( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c) )

• Length * Triangular base area given ii sides and the angle between them (SAS)

  You can calculate area of a triangle easily from trigonometry:

  volume = length * 0.5 * a * b * sin(γ)

• Length * Triangular base of operations area given ii angles and a side between them (ASA)

  You tin calculate that using trigonometry:

  volume = = length * a² * sin(β) * sin(γ) / (2 * sin(β + γ))

Triangular prism surface expanse

If you lot want to calculate the surface area of the solid, the most well-known formula is the one given iii sides of the triangular base :

• area = length * (a + b + c) + (2 * base_area) = length * base_perimeter + (2 * base_area)

Even so, we don't e'er have the three sides given. What then?

• Triangular base: given two sides and the angle between them (SAS)

  Using law of cosines, we can find the third triangle side:

  area = length * (a + b + √( b² + a² - (ii * b * a * cos(angle)))) + a * b * sin(bending)

• Triangular base: given 2 angles and a side betwixt them (ASA)

  Using police of sines, we can find the ii sides of triangular base of operations:

  area = (length * (a + a * (sin(angle1) / sin(angle1+angle2)) + a * (sin(angle2) / sin(angle1+angle2)))) + a * ((a * sin(angle1)) / sin(angle1 + angle2)) * sin(angle2)

The only option when you tin't calculate triangular prism volume is having given triangle base and its height (exercise y'all know why? Think well-nigh it for a moment). All the other versions may be calculated with our triangular prism computer.

Let's bank check what's the book and surface surface area of a tent shaped like a triangular prism:

1. Observe out what'due south the length of the triangular prism. Assume it's equal to 80 in, type this value into the first box of triangular prism calculator.
2. Choose the pick with your parameters given. For example, given three sides of our base of operations.
3. Enter base sides. Our tent has a = lx in, b = fifty in and c = 50 in.
4. Triangular prism surface area and volume appear in no time. It's 96,000 cu in (55.56 cu ft) and 15,200 in² (105.56 ft²).

FAQ

What is a triangular prism?

It is a shape that is formed by wrapping two parallelly faced triangles as top and bottom faces. A triangular prism is a polyhedron with a triangle equally base of operations and rectangles equally lateral faces.

How to draw a triangular prism?

To draw a triangular prism:

1. Draw the base of operations of the prism as a triangle.
2. Draw the top face up of the prism as a triangle parallel to the base.
3. Join the corresponding vertices of both triangles i.eastward., base and top faces.

How many edges do a triangular prism have?

A triangular prism has nine edges, with 3 each forming lesser and elevation faces. The rest of them form the lateral faces.

How many faces do a triangular prism have?

A triangular prism has 5 faces, i.east., a base and top face along with the 3 lateral faces.

How many vertices practice a triangular prism take?

A triangular prism has 6 vertices, i.due east., 3 each on top and bottom triangular faces.

Hanna Pamuła , PhD candidate and Jasmine J Mah

Area of a hemisphere Cube Cube Calc: discover v, a, d … 17 more than

Source: https://www.omnicalculator.com/math/triangular-prism

Posted by: novakdartakifinee.blogspot.com

Share this post